A Guide To Merkle Trees

Introduction

A Merkle tree is a tree founded by Angela Merkel (Chancellor of Germany). Wait...that is something different.🙃

A Merkle tree is nothing but another data structure like a binary tree but with the addition of hash pointers.

Now, you may ask, what is a hash pointer?

The Hash pointers simply point to a place where some data can be stored after being hashed with a cryptographic function to make the data secure. The best example that uses hash pointers is blockchains.

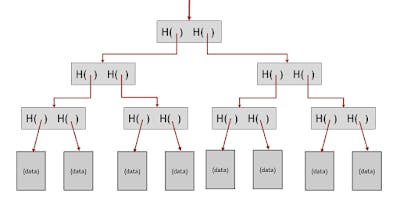
Now coming back to the Merkle tree, data blocks are grouped in pairs and the hash of each of these blocks is stored in a parent node. The parent nodes are in turn grouped in pairs and their hashes are stored one level up the tree. This continues all the way up the tree until we reach the root node.

If an adversary tampers with any data block at the bottom of the tree, that will cause the hash pointer that’s one level up to not match, and even if the person continues to tamper with this block, the change will eventually propagate to the top of the tree where they won’t be able to tamper with the hash pointer that we’ve stored.

The below diagram explains the structure:

Use Case

Let's now see the use cases. There are three major systems that use the Merkle tree as one of their implementations:

GIT
Amazon Dynamo DB
Blockchain

Let's have a look into one of the use cases of Merkle trees which is Amazon DynamoDB:

Amazon's Dynamo DB is one of the NoSQL databases which consists of the many nodes in a cluster and these nodes are continuously performing consistent hashing which is a special kind of hashing such that when the hash table is resized only K/n keys need to be remapped where 'K' is the number of keys and 'n' is the number of slots, unlike most traditional hash tables where a change in a number of slots causes all keys to be remapped.

Now in order to do consistent hashing, we require data migration and at the same time. We also want to minimize this data migration.

What do think will help in this case?

This can be achieved using Merkle trees while checking for inconsistencies among replicas (Merkle trees minimizes the amount of data transfer for synchronization).

Each node maintains a separate Merkle tree for each key range (the set of keys covered by a virtual node) it hosts. This allows nodes to compare whether the keys within a key range are up-to-date. In this scheme, two nodes exchange the root of the Merkle tree corresponding to the key ranges that they host in common.

Subsequently, using the tree traversal scheme described above the nodes determine if they have any differences and perform the appropriate synchronization action. The sole disadvantage with this scheme is that many key ranges change when a node joins or leaves the system thereby requiring the tree(s) to be recalculated.

Advantages of Merkle Tree

Tree can hold hash but just need to remember the hash of the root.
Can verify the membership in O(log N) time.
Sorted Merkle trees where blocks are ordered at the bottom can verify non membership in O(log N)
Proof of non-membership: Simply by showing a path to the item that's just before where the item in question would be and showing the path to the item that is just after where it would be.

Time Complexity of the various operations

Search O(log N)
Traverse O(n)
Insertion O(n)
Deletion O(n)

Merkle Tree

Comments (2)

Blockchain & Crypto

Welcome to the World of 'NFTs'

More from this blog

How to Size Java Database Connection Pools in Kubernetes

What is Jib? A Complete Guide to Java Containerization Without Dockerfiles

Kafka Consumer Container Restarts in Kubernetes: A Production Case Study

How we solved cache invalidation in Kubernetes with a headless service

Going Vernacular: Engineering Our Way to Process Multilingual Names

Introduction

Use Case

Advantages of Merkle Tree

Time Complexity of the various operations

Command Palette

Comments (2)

Blockchain & Crypto

Welcome to the World of 'NFTs'

More from this blog

Introduction

Use Case

Advantages of Merkle Tree

Time Complexity of the various operations