A lot of time you will come across a problem in computer science when you want to find whether an element is present in a set of already existing elements. For example, if I want to know whether the word "cat" is present in our database which is say, storing the names of various animals. The first and easiest approach that comes to mind is to simply do this -
SELECT * FROM db_animals WHERE name='cat'
This approach however will take O(n) which is good if the number of rows in our table is limited to some extent but imagine we have millions and billions of records, now the same query will take forever to return the result (assuming we don't index the name column).
This is the reason we wanted something that could tell us if a record is present in the set of billions of elements quickly, that's when bloom filters come.
Bloom filter is a probabilistic data structure which was given by Burton Bloom in 1970 which will return whether an element is "possibly in a set" or "definitely not in a set". Bloom filters reduce the expensive disk lookups in case the element is not present hence it is efficient to use them for large-scale use cases.
How does Bloom filter Work?
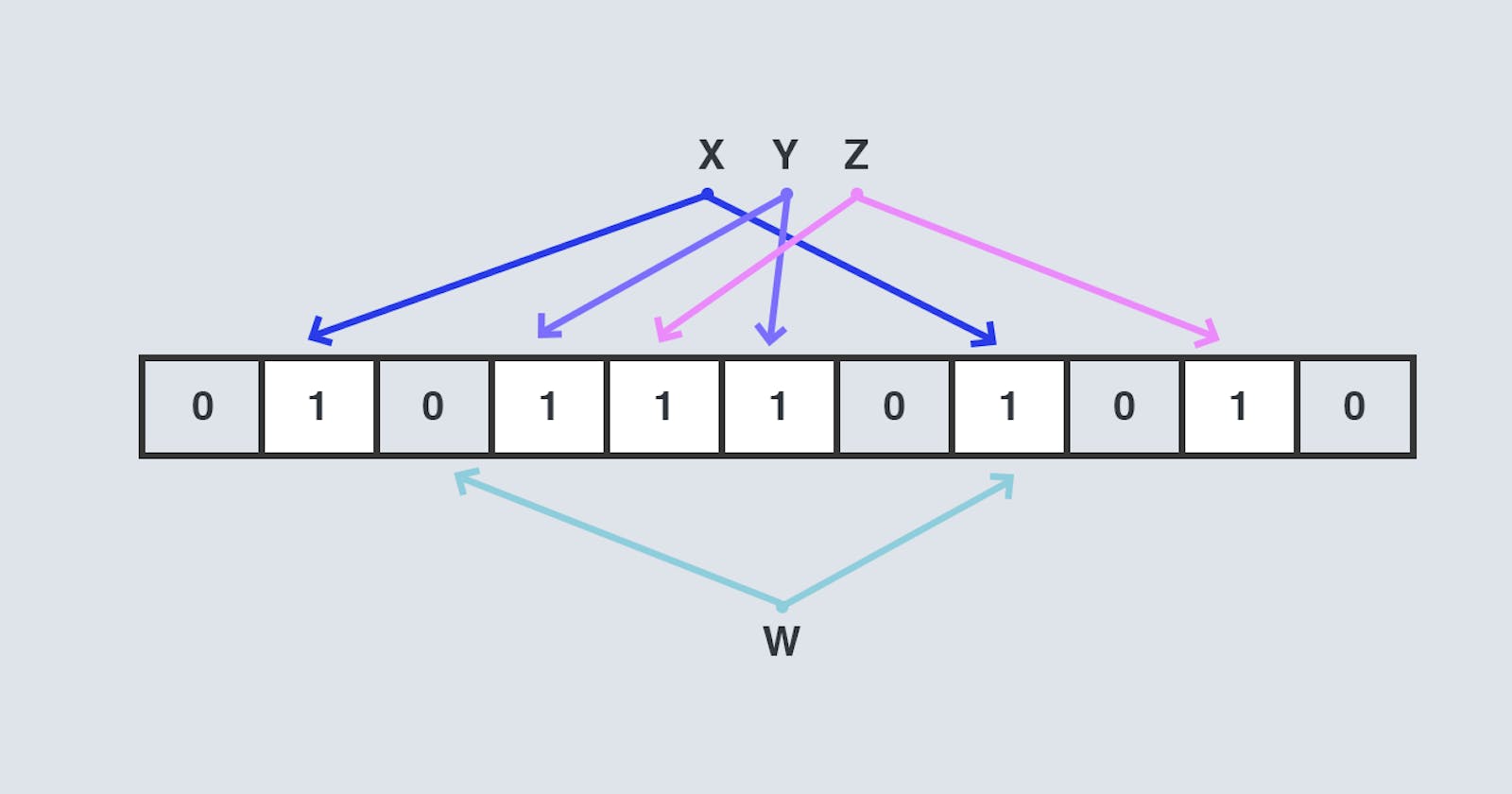
Take a binary array of 'm' bits initialized with 0 for up to n different elements, set 'k' bits to 1 in the position chosen by the output of all the n different elements after passing through hash functions. Now take the element you want to identify if it is already present or not. Pass it through the same hash function, if all bits are set, the element probably already exists, with a false positive rate of p; if any of the bits are not set, the element certainly does not exist.
I know it sounds weird if you are reading it the first time so let me simplify it a little:
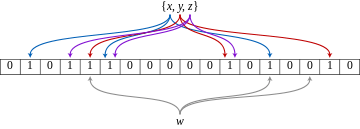
Suppose I have 3 hash functions f(x),f(y),f(z), and a database to store the animal names, every time a user gives me a name to save it will have to pass through all the 3 hash functions.
The output of these 3 hash functions generates 3 different numbers which I will treat as the index of my binary array of size say 128 bit initialized with 0 and set the bits to 1 at those 3 indexes I got as a result of my hash functions.
Now, if a search query comes, I will again pass the parameter of that search query to the same 3 hash function (this process is also known as membership testing) which will return me 3 indexes. If I find 0 even at any one of the positions I can definitely say that the element is not present but if I find 1 at all positions then it may or may not be present this is why bloom filters are known as probabilistic data structures.
Now the question is how accurate these bloom filters are i.e if it says the element is present then what is the probability that the element is NOT present. And another question is how are these efficient compared to other approaches.
How fast and space efficient is a Bloom filter?
Given a Bloom filter with k hashing functions, both insertion and membership testing then take O(k). That is because, each time you want to add an element to the set or check set membership, you just need to run the element through the k hash functions and add it to the set or change those bits to 1.
So, the time complexity is pretty good compared to the naive approach of O(n) where n is the number of elements present already.
Generally, if you know how many elements you're going to store on a prior basis, it is easier for you to determine what would be the size of your bit array(m) otherwise you need to make a wild guess if you do not know or cannot approximate the number of items. You could put an arbitrarily large size, but that would be a waste in terms of space which we are trying to optimize in the very first place.
In fact, you should only choose bloom filter when you know the total elements(n) that you are going to insert, this way you can calculate the efficient value of m(less than 'n') hence saving space.
Probability of false positives
Generally speaking, fewer than 10 bits per element are required for a 1% false-positive probability, independent of the size or number of elements in the set. We have two choices of parameters when building a bloom filter, m, and k. They should each be chosen to decrease the probability of false positives as much as possible.
If we have a bloom filter with m bits and k hash functions, the probability that a certain bit will be one after feeding the element with k hash functions is: (1/m)^{k}
Therefore, the probability that a certain bit will still be zero after one insertion is: (1 - 1/m)^{k}
Then, after n insertions, the probability of it still being zero after n insertions are: (1 - 1/m)^{nk}, let's call this 'X'
What we are interested in is the error rate i.e the probability of us going wrong which is the probability of getting k times the value 1 in succession So, that means the probability of a false positive is: (1 - (1 - 1/m)^{nk})^{k} or (1-X)^{k}
This equation is what we need. Now, let's do some observation and evaluate some values out of the final equation:
Assume m tends to ∞ then value of X->1 and the final equation yields (1-1)^{k} which is 0, this implies that if the size of our bit array becomes infinite the error we get is 0. Now assume m=1 then X=0 and the probability of error becomes 1 i.e 100% which is obvious because we have only one place to store the bits and the second time anything comes it will also have to go to the same index.
If you play around with the equation by giving some arbitrary values to m for a given k you will notice that the error rate keeps on decreasing till a certain point after which it again starts increasing, which means for a particular value of 'k' there is a fixed value of 'm' for which we have the minimum error rate. This can also be proved if you do the differentiation of the final equation we got.
Also if you notice In the equations, raising the value of 'k' (the number of hash functions) will make the probability of a false positive less likely. However, it is not computationally efficient to have an enormous value for 'k'.
To minimize this equation, we must choose the best 'k'. We do it this way because we assume that the programmer has already chosen an mm based on their space constraints and that they have some idea what their potential n will be. So the k value that minimizes that equation is: k = ln(2)*(m/n) .
If you want to explore this in more detail then here is the website which helps you choose the optimal value for your filter.
Application of bloom filters
Apache Cassandra and PostgreSQL use Bloom filters to reduce the disk lookups for non-existent rows or columns. Avoiding costly disk lookups considerably increases the performance of a database query operation.
The Chrome web browser used to use a Bloom filter to identify malicious URLs. Any URL was first checked against a local Bloom filter, and only if the Bloom filter returned a positive result was a full check of the URL performed (and the user warned, if that too returned a positive result).
Bitcoin uses Bloom filters to speed up wallet synchronization.
Medium uses Bloom filters to avoid recommending articles a user has previously read.
Implementation
I have implemented a basic bloom filter in python you can have a look at it here => Bloom Filter Implementation.