Debunking YOUR Basic Math Concepts
Can you guess the sum of all natural numbers?
Sum of all positive integers
What is 1+2? Ah, who doesn't know, it’s 3. What is 1+2+3? Well, it’s 6. (easy peasy lemon squeezy)
Now, what if I asked you to count the sum of all positive integers which is: 1+2+3+4…to infinity?
That's it. This is the crux of this blog post.
Wait a minute, what?
All positive numbers when add up together should be infinite, right?
But now what if I tell you, there is a definite answer for this and it's not something indefinite like infinity. It has a fixed value assigned to it🤯
In this blog post, I will give you the Most Astonishing Proof In Mathematics: Which is the sum of all natural numbers is equal to -1/12.
That looks very wrong. You must be thinking that this is some kind of typo, right? Well, let me assure you that it’s very much intentional!
The sum of all natural numbers IS EQUAL to -1/12.

As a matter of fact, this equation is actually a very important result used in theoretical physics, particularly in string theory.
I am sure y'all are having so many questions right now. How come the sum of positive numbers results in a negative number? What is the proof behind this? Do we ever encounter it in real life?
We will answer these questions one by one
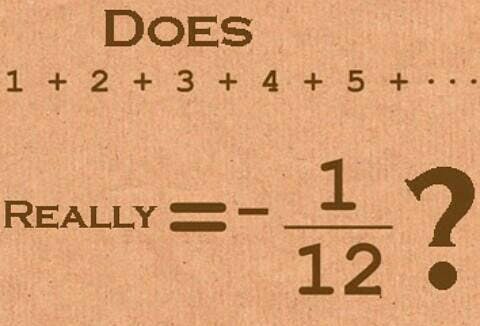
The Proof
The proof is rather simple. Before we get to that, let us try and understand a couple of other series first -
Consider the following infinite summation (X):
X = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 ...
Rearranging the above equation, we get:
X = 1 - (1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 ...)
If you look at the term inside the brackets, you will realize it is our original series 'X'. So let’s substitute that:
X = 1 - X
2X = 1
X = 1/2
Hope this is clear, BTW this is also known as Grandi's series
Now let’s consider another summation (Y) :
Y = 1 - 2 + 3 - 4 + 5 +6 ... -A
Writing it in another way by adding 0 to both sides, we get:
0 + Y = 0 + 1 - 2 + 3 - 4 + 5 + 6...
or simply,
Y = 0 + 1 - 2 + 3 - 4 + 5 + 6... -B
Adding the two equations A + B:
Y + Y = (1 - 2 + 3 - 4 + 5 ...) + (0 + 1 - 2 + 3 - 4 + 5 ...)
Grouping the corresponding terms within the brackets, we get:
2Y = 1 + 0 - 2 + 1 + 3 - 2 - 4 + 3 + 5 - 4 ...
2Y = 1 - (2-1) + (3-2) - (4-3) + ...
2Y = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1...
But the summation on the right-hand side is X as we previously saw, so let’s substitute it:
2Y = X
2Y = 1/2
Y = 1/4
Finally, let’s consider our original series i.e. the sum of all natural numbers:
S = 1 + 2 + 3 + 4 + ...
We defined Y earlier as:
`Y = 1 - 2 + 3 - 4 + ...
Subtracting Y from S:
S - Y = 1 - 1 + 2 + 2 + 3 - 3 + 4 + 4 + ...
S - Y = 4 + 8 + 12 + 16 + ...
We just calculated the value of Y which is equal to 1/4. So let’s substitute it:
S - 1/4 = 4 x (1 + 2 + 3 + 4 + ...)
S - 1/4 = 4S
3S = -1/4
S = -1/12
So there we go! We now have the proof.
Looks like a clever maneuver. Is this a mathematical trick?
The answer is No.
It actually appears in many areas of physics.
The only thing to notice here is that we are applying regular algebra rules to a divergent infinite series.
A convergent series is the one in which the sum keeps converging to a particular definite number as you keep adding more numbers to it. Divergent series is the opposite of that. We will discuss more about it in the next part of this blog post.
What is the logical explanation of this counterintuitive proof?
It makes absolutely no sense to keep adding positive numbers and get the negative result, right?
But this is only valid if we were not dealing with infinity!
Here, we are dealing with what is called an infinite series, a sum that goes on forever.
The sums can be grouped into 2 categories –
- Convergent
- Divergent.
A convergent series is a summation that converges to a finite value.
A divergent series is a summation that diverges to a larger value (infinity). The series 1+2+3+4+… is a divergent sum because it becomes bigger and bigger until it reaches infinity.

The concept of infinity is very obscure. When you think of a series of numbers and their summations, you tend to get inclined to think in terms of convergent series.
When we are dealing with divergent series, things get a bit tricky.
First of all, the algebraic rules that apply to regular numbers do not apply to non-converging infinite sums.
Secondly, you cannot keep adding values until infinity because you will never get there. All of the sums we discussed above are diverging infinite sums, so regular algebraic rules do not apply.
But mathematicians and physicists don’t like the concept of “getting nowhere” they want a definitive answer for every question. So, they have implemented ways to define the sums of non-converging infinite series.
The one that we just discussed is called Ramanujan summation.
Is this result ever useful in the real world?
All the mathematics aside, one might wonder whether or not this result is useful in real life.
The answer turns out to be YES.
In some scenarios, this approach gives the correct result in a real-world problem, even though it looks mathematically “wrong”.
A simple example is the Casimir effect.
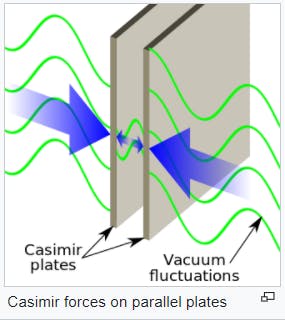
Let’s say we place two metal plates a very short distance apart (in a vacuum with no gravity, assuming ideal physics conditions).
Our classical physics predicts they will just be still with no force in action. However, there are studies that say that there's actually a small attractive force between them.
This, however, can be explained using quantum physics, and calculation for the magnitude of the force uses the Ramanujan summation that we just discussed.
Learn more about it here.
In the Casimir effect, the “regular” physics approach is unable to explain this scenario. This is why, sometimes, complex counterintuitive mathematical formulations are needed to explain simple things.
Conclusion
The only conclusion is if someone is giving you money every day and they keep on increasing a unit each day, they are actually fooling you and making you poor 😜
Oh, BTW this blog post was inspired from the Numberphile Video 🎥
Thanks for reading :))

